… and we’re back on the question of “how small a solder powder particle do I need, to achieve a certain bump height or bump diameter”?. There are a lot of factors that control this, but after taking the metal loading and other, second order, variables out of the picture, the two main questions to be answered are:
- How big is the bump (width or height)?
- What is your allowable bump height / diameter variability?
As solder bump dimensions shrink, the finite size of the particles in the solder paste used to form that bump affects the final solder bump variability. See the figure below for a visual description: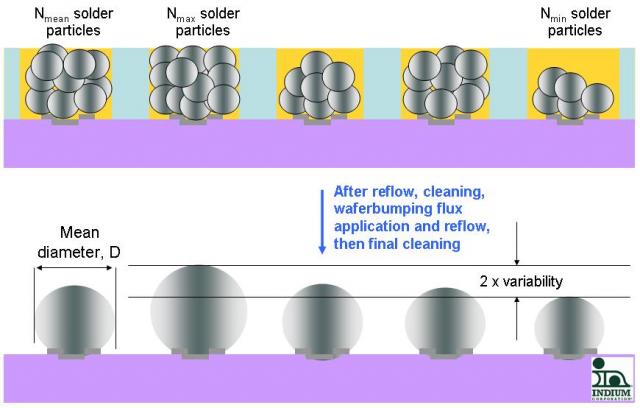
The variability therefore comes from each solder paste deposit containing a certain number of solder particles; more or less solder particles than the one next to it and so on. The question then is: how many solder particles (n), and of what diameter (d)?
Note that n = [N(max)-N(min)] / 2
You can see the effect of this in the enclosed table: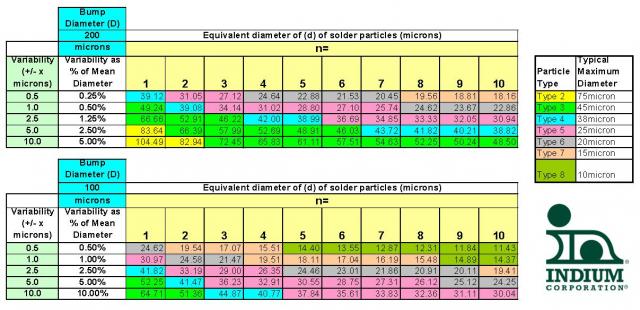
For example, from the above table, for a bump diameter of 200microns and allowable variability of 5microns (2.5%) across the substrate, if the number of solder particles in each deposit can vary by up to 2 (n=2), then type 3 powder will be sufficient. If the printing process gives you a large variation from deposit to deposit - as much as 10 particles perhaps (n=10) - then type 4 powder will be needed.
I'd like to propose a new guideline (Mackie's Rule) to go with the previous two, and say that a good overestimate of the solder powder type needed for bumps of mean diameter D, and a certain desired variability, should be based on plus or minus the volume of five (n=5) solder powder particles of the largest expected diameter for a powder of that type.
Lots of questions remain - probably most critically:
1/ Variability: How do you define variability, assuming a Gaussian distribution of bump diameters? 2 sigma; 3 sigma?.
2/ Print Process: Also note that this Rule is based on the FCI "drive-in" process discussed last time. Release of solder paste from the stencil will increase the variability, and also (critically) make it time dependent, due to the thixotropy of the paste.
3/ Can the bump diameter be used as a reasonable estimate of a spherical bump?
I am looking forward to someone proving me wrong, but at least we have a basis for recommendations.
Also, many thanks to Ron Lasky for pointing out the absence of clarity in the original description of the approach above.
Cheers! Andy


